О разделении суммы средневозвратного процесса и случайного блуждания

Введение

Увы, одна очень интересная тема, как мне показалось, была обделена вниманием смартлабовцев. В ходе обсуждения этой темы мною была озвучена (в общем-то, очевидная) идея: найти разложение цены на трендовый и средневозвратный процесс, либо на средневозвратный процесс и случайное блуждание; отделённый от остальной динамики средневозвратный процесс может служить источником сигнала для контр-трендовой стратегии.

Вашему вниманию предлагается небольшое исследование, в котором будут рассмотрены:

1) Несколько видов случайных процессов:
ABM: арифметическое Броуновское движение без сноса, на котором невозможно заработать;
OU: процесс Орнштейна-Уленбека, являющийся средневозвратным, и на котором можно заработать;
Independent.ABM+OU: сумму арифметического Броуновского движения и процесса Орнштейна-Уленбека с некоррелированными инновациями, которое можно рассматривать как модель цены для построения контр-трендовой стратегии;
Correlated.ABM+OU: сумму арифметического Броуновского движения и процесса Орнштейна-Уленбека с коррелированными инновациями, которая обладает более интересными свойствами;
2) Структурные функции вышеуказанных случайных процессов, теоретические (за исключением случая Correlated.ABM+OU) и эмпирические (во всех случаях);
3) Численный способ оценивания параметров Independent.ABM+OU на основе эмпирической структурной функции, а также немного рассуждений про способы оценивания параметров для случая Correlated.ABM+OU;
4) Использование фильтра Калмана для оценивания каждой из компонент, входящих в процессы Independent.ABM+OU и Correlated.ABM+OU.

В конце статьи вы найдёте ссылку на код на языках R и C++, который использовался для выполнения численных экспериментов.

И, разумеется, в статье будет куча формул. Ещё не поздно закрыть вкладку! :)

Арифметическое Броуновское движение, процесс Орнштейна-Уленбека и их структурные функции

Арифметическое Броуновское движение (ABM) описывается стохастическим дифференциальным уравнением (СДУ) вида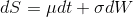 , где 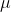— снос, 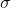— волатильность, а 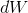— дифференциал стандартного Винеровского процесса. В рамках этой статьи я буду рассматривать лишь случай 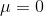, т.е. арифметическое Броуновское движение вида 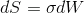. Решение этого СДУ имеет вид . Главное, что нужно знать об этом процессе — что на нём не существует прибыльных торговых стратегий.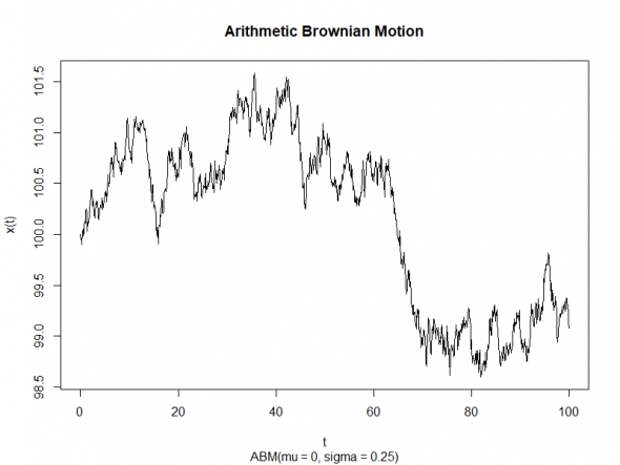


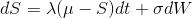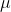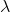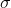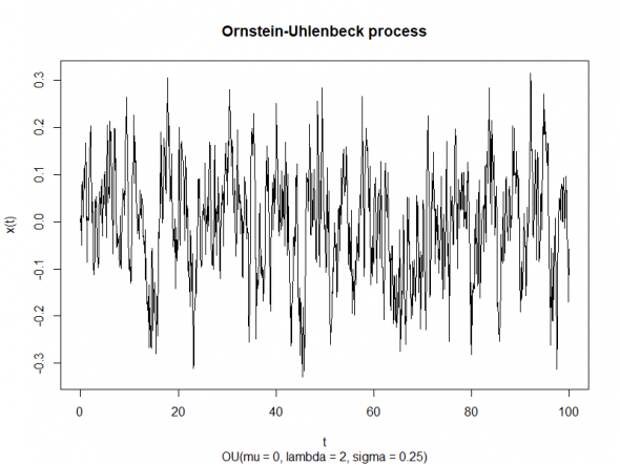
Процесс Орнштейна-Уленбека (OU) описывается СДУ вида , где  — среднее, к которому возвращается процесс,  — скорость возврата процесса к среднему (чем больше — тем быстрее; нулевое значение превращает процесс Орнштейна-Уленбека в арифметическое Броуновское движение), — волатильность. Решение этого СДУ имеет вид .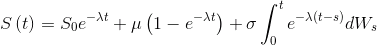


Ниже представлен код для генерации траекторий процессов ABM и OU:


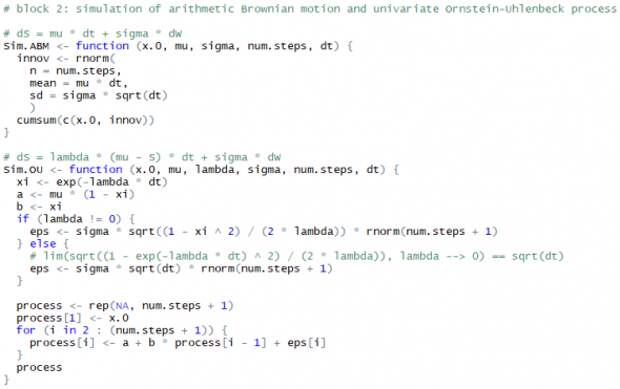
Структурная функция случайного процесса со стационарными приращениями определяется следующим образом: 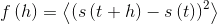; случайная величина, стоящая в треугольных скобках, подвергается усреднению. Ниже представлены функции для расчета эмпирической структурной функции по реализации случайного процесса, а также функции для их визуализации: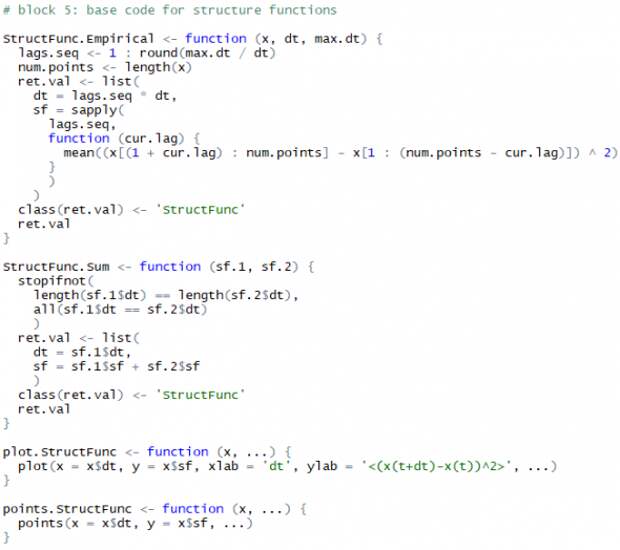

Структурная функция арифметического Броуновского движения  имеет вид 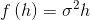. Структурная функция одномерного процесса Орнштейна-Уленбека имеет вид 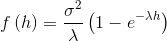, причём 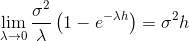, что совпадает со структурной функцией ABM. Ранее было отмечено, что при обращении скорости возврата  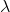в ноль — процесс OU превращается в ABM. Очевидно, что зная эмпирическую структурную функцию процесса, можно попробовать подобрать параметры процессов OU и ABM (разумеется, этими двумя дело не ограничивается), минимизируя по параметрам отклонение теоретической функции от эмпирической.

Ниже представлен код, реализующий численный расчёт указанных структурных функций:

Ниже представлены графики структурных функций для арифметического Броуновского движения и процесса Орнштейна-Уленбека. Красными звёздочками изображены эмпирические структурные функции, полученные из неких реализаций соответствующих процессов. Черными линиями изображены теоретические структурные функции для тех же значений параметров, которые использовались для генерации реализаций и вычисления эмпирических структурных функций.

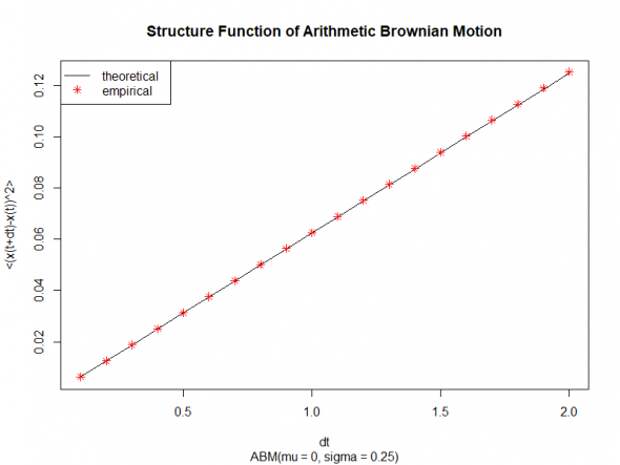
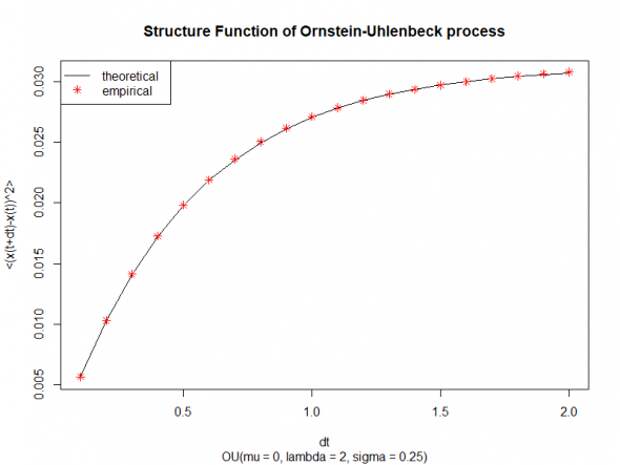
Сумма арифметического Броуновского движения и процесса Орнштейна-Уленбека с некоррелированными приращениями (Independent.ABM+OU)

Рассмотрим случайный процесс Independent.ABM+OU, являющийся суммой арифметического Броуновского движения и процесса Орнштейна-Уленбека, и характеризующегося набором параметров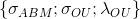 — волатильностями ABM и OU частей, а также скоростью возврата OU части к среднему (которое равно нулю). Его динамика описывается системой СДУ вида
;
;
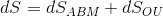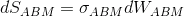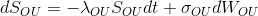, причём
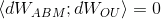— Винеровские процессы, входящие в ABM и OU части, независимы.

Численное моделирование процесса можно выполнять моделированием входящих в него компонент с последующим их сложением.

Структурная функция полученного процесса имеет вид 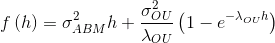. Убедимся в этом:



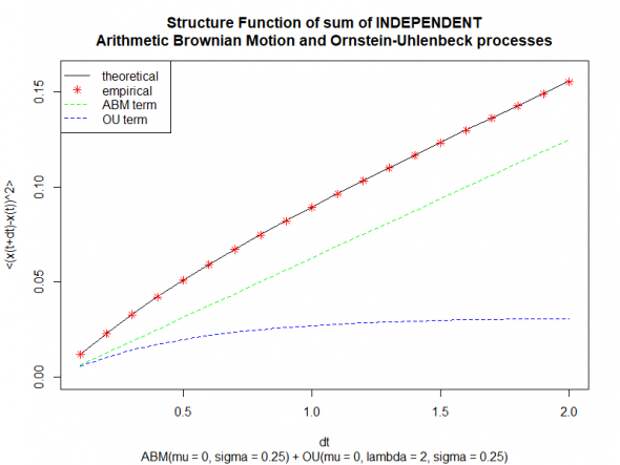
На предыдущем графике:
— красными звездочками изображена эмпирическая структурная функция некоторой реализации процесса Independent.ABM+OU;
— чёрной линией изображена теоретическая структурная функция вида 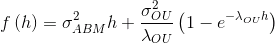, с теми же параметрами, которые использовались при генерации реализации случайного процесса;
— зелёной и синей линиями изображены теоретические структурные функции компонент ABM и OU, соответственно.

Построим процедуру численного оценивания параметров процесса Independent.ABM+OU путём подгонки его теоретической структурной функции к эмпирической структурной функции некоторого процесса. В качестве критерия оптимизации будем использовать сумму квадратов ошибок.
Одним из нюансов, которые нужно учесть, является превращение процесса OU в процесс ABM при 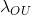равном нулю. В этом случае нужно чуть иначе считать теоретическую структурную функцию из-за возникающего деления на ноль. Кроме того, если в результате оптимизации получилось оптимальное значение  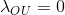— перенесём всю волатильность в процесс ABM, воспользовавшись правилом сложения дисперсий. Отделение арифметического Броуновского движения от процесса Орнштейна-Уленбека в этом случае будет невозможным.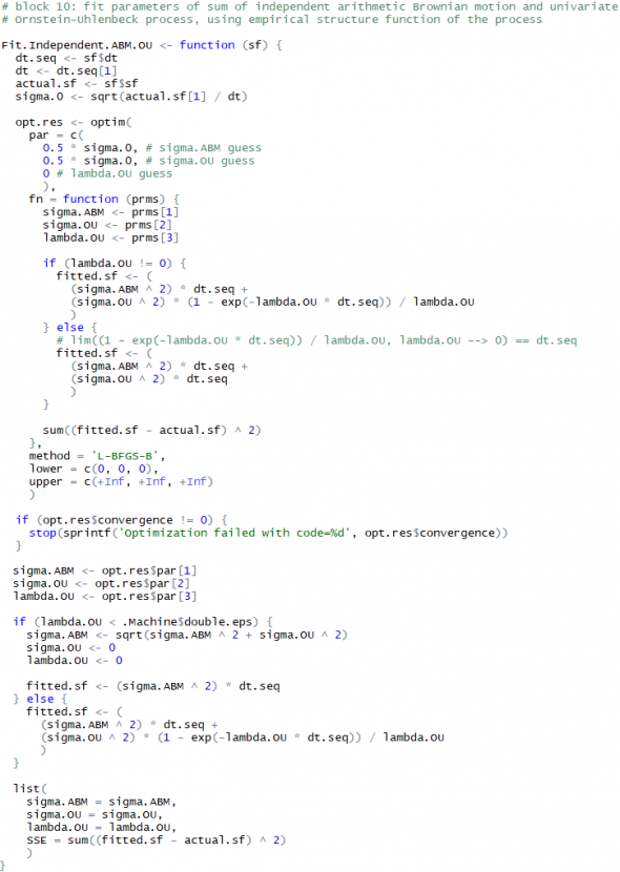



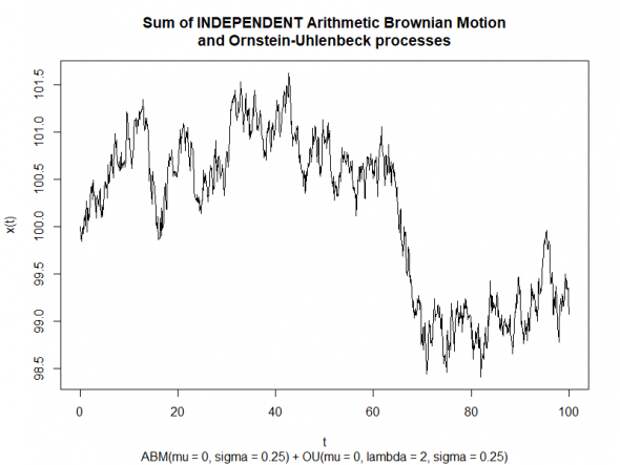
Приведём небольшой пример реализации процесса Independent.ABM+OU. Визуальное отличие от исходного ABM процесса, представленного ранее, практически не заметно. Однако статистическая разница присутствует и мы сможем приблизительно разделить процесс на составляющие его компоненты.


Воспользуемся разработанной ранее процедурой для оценивания параметров процесса 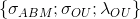 по эмпирической структурной функции: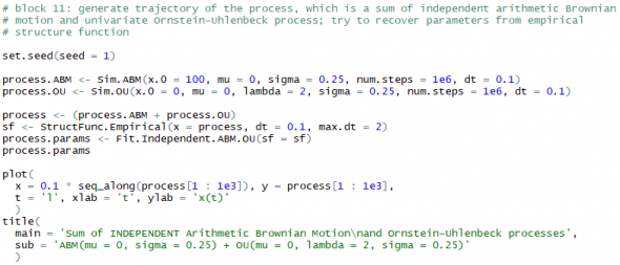

В результате получим оценки значений параметров, равные 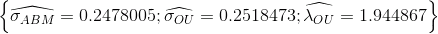 при истинных значениях параметров .

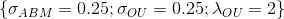Использование фильтра Калмана для разделения суммы арифметического Броуновского движения и процесса Орнштейна-Уленбека с некоррелированными приращениями (Independent.ABM+OU) на компоненты

Для дальнейшей работы нам потребуется фильтр Калмана. В репозитории CRAN представлено множество его реализаций: FKF, KFAS, KFKSDS, miscFuncs, RAHRS, dlm, не считая встроенных (?stats::KalmanLike). Пользоваться мы ими, конечно же, не будем.

В иллюстративных целях подойдёт примитивная и минимально функциональная реализация (только шаги predict & correct, без оценивания параметров при помощи MLE):



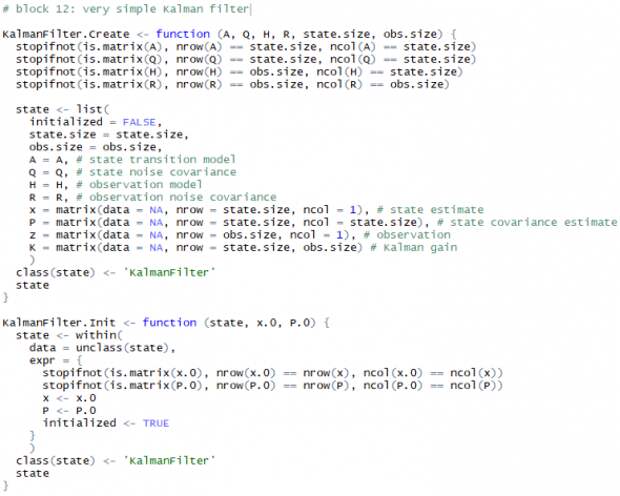
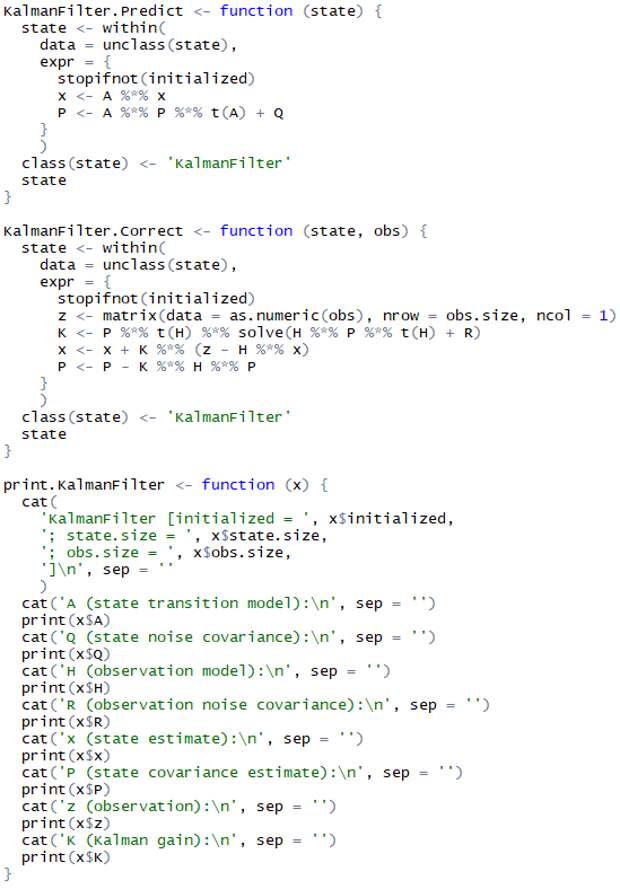
В данной реализации фильтра Калмана используется линейная динамическая система:
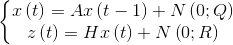, где:
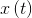— вектор состояния системы (ненаблюдаемые переменные, значения которых мы хотим оценить);
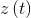-  вектор наблюдаемых переменных системы;
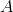— матрица, задающая детерминированную часть динамики состояния системы;
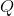— матрица ковариации шума, воздействующего на состояние системы и имеющего многомерное нормальное распределение с нулевым средним;
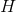— матрица, задающая преобразование ненаблюдаемого состояния системы в наблюдаемые переменные;
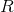— матрица ковариации шума, воздействующего на наблюдаемые переменные системы и имеющего многомерное нормальное распределение с нулевым средним.
Помимо оценки ненаблюдаемого состояния системы 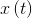, фильтр Калмана также предоставляет оценку ковариации ненаблюдаемого состояния системы .

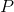Чтобы построить фильтр Калмана, способный разделять компоненты процесса Independent.ABM+OU, требуется задать матрицы 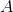, , 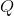, 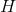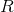. Они легко вычисляются из ранее оцененных параметров процесса :

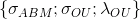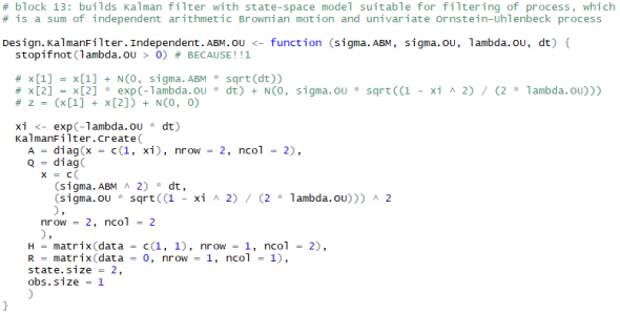
Диагональ матрицы перехода состояния 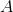 и матрицы ковариации шума состояния  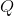фактически представляют собой части функций, которые использовались для численного моделирования процессов ABM (Sim.ABM(…)) и OU (Sim.OU(…)). Матрица преобразования состояния в наблюдаемые переменные состоит из двух единиц, тем самым получаем, что наблюдаемый процесс является суммой процессов ABM и OU, являющихся компонентами вектора состояний.

Инициализируем фильтр Калмана в соответствии с разработанной динамической системой, а также параметрами, оцененными из эмпирической структурной функции процесса, после чего запустим фильтр, записывая его оценки скрытого состояния динамической системы.


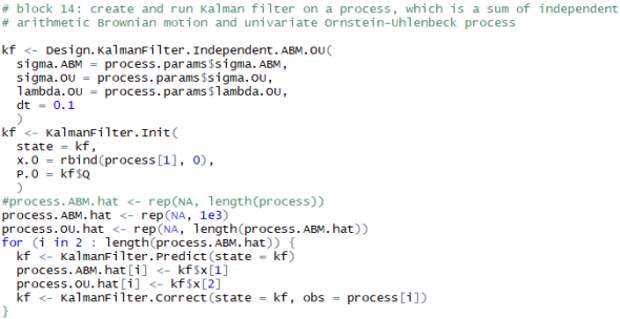
Ниже представлен график реализации процесса Independent.ABM+OU (чёрный), оценки ABM компоненты фильтром Калмана (красный) и истинного значения ABM компоненты (зелёный). На нём видно… что ничего не видно.


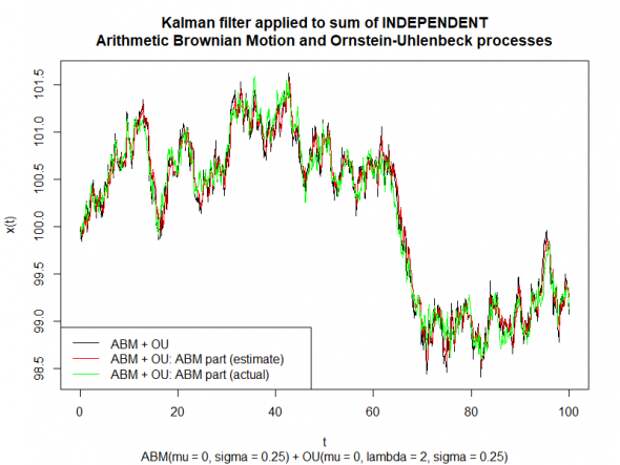
Ниже представлен график оценки OU компоненты фильтром Калмана (красный) и истинного значения OU компоненты (зелёный).


Построим scatter plot на основе данных с предыдущего графика:

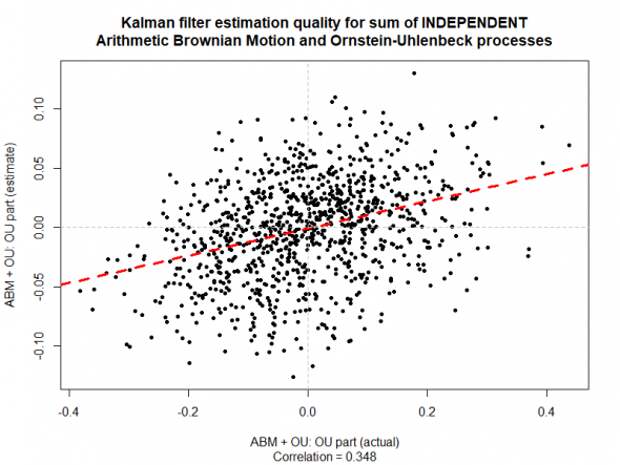
На представленном графике видно, что между истинным значением средневозвратного процесса OU и оценкой, полученной при помощи фильтра Калмана, имеется существенная корреляция. Разработанную методику можно попробовать применить, чтобы разложить аналогичным образом логарифм цены некоторого инструмента (портфеля инструментов).

Сумма арифметического Броуновского движения и процесса Орнштейна-Уленбека с коррелированными приращениями (Correlated.ABM+OU)

Пусть теперь Винеровские процессы, входящие в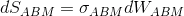 и 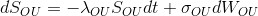, будут коррелированы. Генерировать траектории ABM и OU компонент по-отдельности теперь не получится. Как ранее было сказано, при  равном нулю, процесс OU превращается в процесс ABM. Тогда для моделирования процесса Correlated.ABM+OU можно использовать многомерный процесс Орнштейна-Уленбека (MvOU): 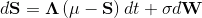, где:
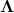— вещественная матрица, отвечающая за скорость возврата к среднему;
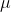— вектор средних, к которым происходит возврат;
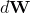— дифференциал многомерного стандартного Винеровского процесса;
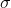— вещественная матрица, такая что 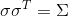, где 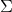 — матрица ковариаций (мгновенных).

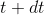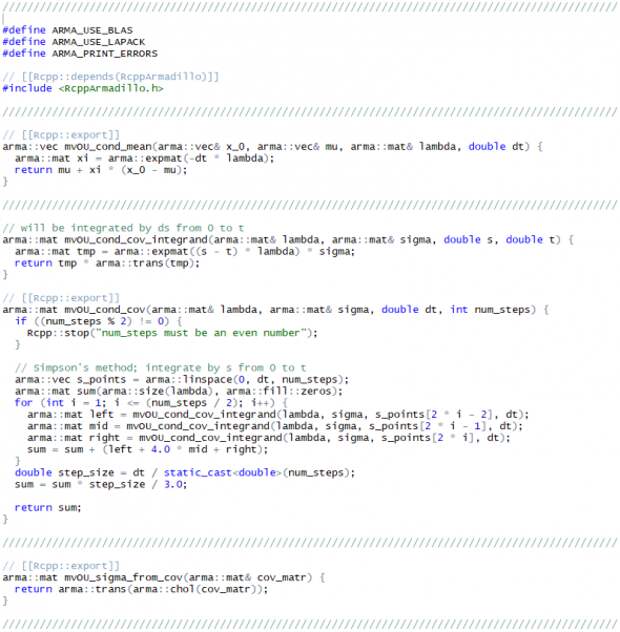
Для генерации такого процесса нам потребуются условные матожидание и ковариация многомерного нормального распределения, из которого будем брать приращения для получения значения процесса в момент исходя из известного значения в момент 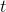. Расчёт данных параметров был реализован на C++, т.к. пакет RcppArmadillo предоставляет удобную и быстродействующую библиотеку матричной алгебры:

(файл MvOU.cpp)


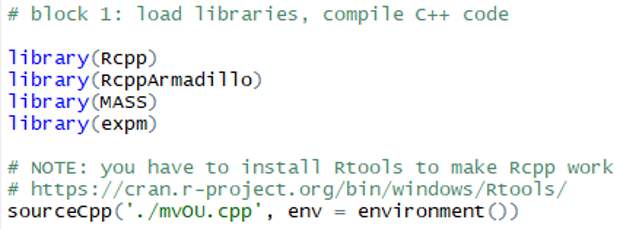
Код, загружающий необходимые пакеты, а также выполняющий компиляцию C++ кода:


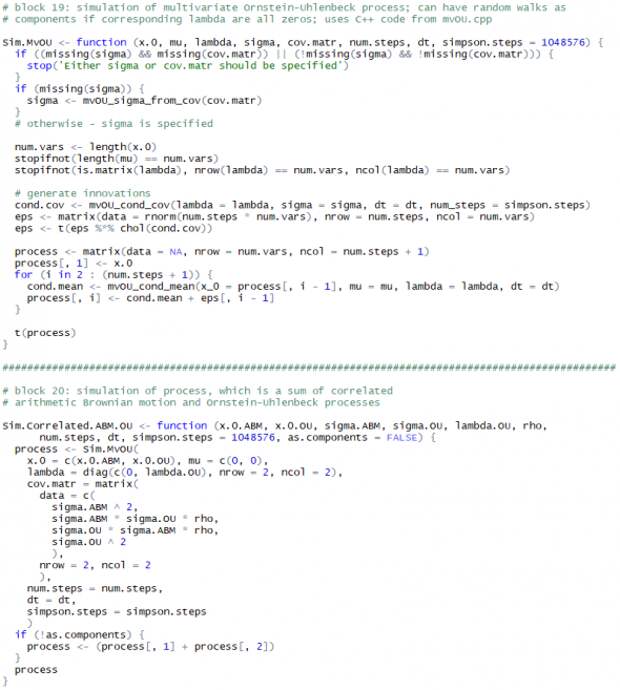
Тогда моделирование многомерного процесса Орнштейна-Уленбека (MvOU) и процесса, являющегося суммой коррелированных арифметического Броуновского движения и одномерного процесса Орнштейна-Уленбека (Correlated.ABM+OU), как частного случая MvOU, выполняется следующим образом:


Ниже представлен график реализаций процесса Correlated.ABM+OU для значений корреляции между инновациями компонент, равных 0 (чёрная), +0.9 (красная) и -0.9 (зелёная):


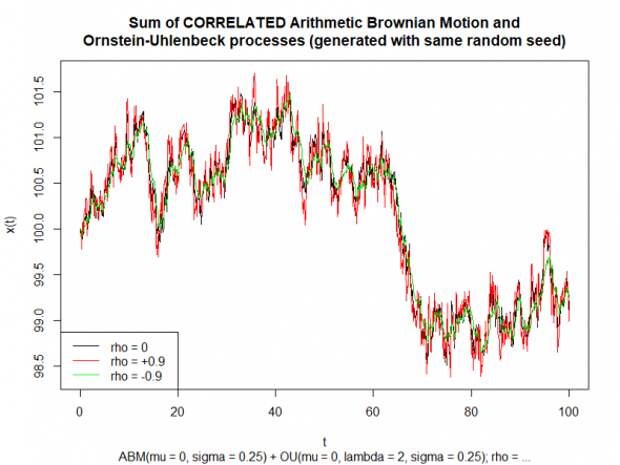
Видно, что при положительной корреляции за шоками следуют более сильные откаты (процесс становится более антиперсистентным, чем Independent.ABM+OU), а при отрицательной — влияние шоков сглаживается во времени (процесс становится более персистентным, чем Independent.ABM+OU).

Построим эмпирические структурные функции этих реализаций процесса Correlated.ABM+OU, и сравним их с теоретической структурной функцией процесса Independent.ABM+OU, а также теоретическими структурными функциями его компонент:


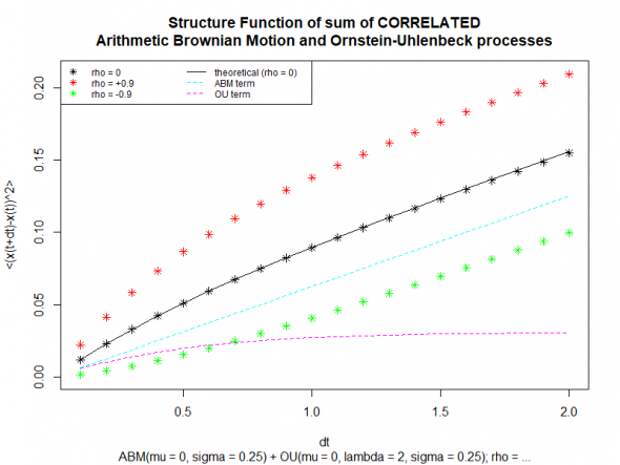
Возникает подозрение, что на основе анализа эмпирической структурной функции процесс Correlated.ABM+OU легко спутать с обобщённым Броуновским движением (СДУ: 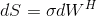; теоретическая структурная функция: 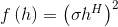, где 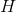— показатель Хёрста). Попробуем подогнать теоретическую структурную функцию обобщённого Броуновского движения (GenBM) к эмпирическим структурным функциям реализаций Correlated.ABM+OU: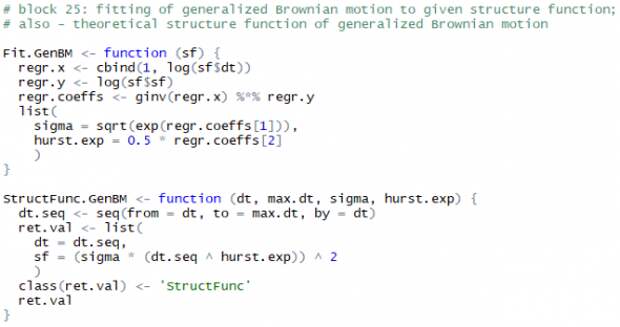



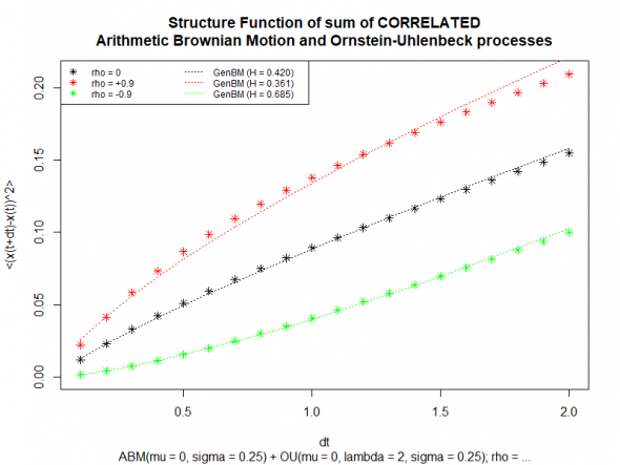
Несмотря на то, что даже в случае нулевой корреляции структурная функция имеет вид 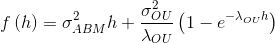, не соответствующий виду структурной функции GenBM — на графике видим неплохое совпадение. Т.е. на небольшом кол-ве, либо на зашумленных данных, имеем все шансы спутать такие процессы.

Построим зависимость показателя Хёрста, которому хорошо соответствуют эмпирические структурные функции процесса Correlated.ABM+OU, от корреляции между инновациями компонент процесса:


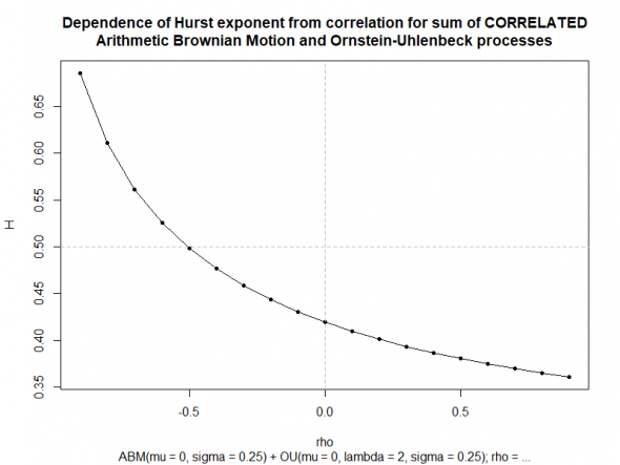
Что касается оценивания набора параметров 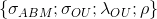 процесса Correlated.ABM+OU, есть такие варианты:
1) Аналитически вычислить структурную функцию многомерного процесса Орнштейна-Уленбека и подогнать её по параметрам под эмпирическую;
2) Составить модель для фильтра Калмана и использовать на ней метод максимального правдоподобия;
3) Численно оптимизировать по параметрам, генерируя для каждого из проверяемых набора параметров реализацию процесса и вычисляя его эмпирическую структурную функцию; в качестве критерия оптимизации использовать сумму квадратов разностей между эмпирической структурной функцией целевого процесса и эмпирической структурной функцией процесса, смоделированного на основе текущих параметров.

Использование фильтра Калмана для разделения суммы арифметического Броуновского движения и процесса Орнштейна-Уленбека с коррелированными приращениями (Correlated.ABM+OU) на компоненты

Составим функцию для инициализации параметров линейной динамической системы в основе фильтра Калмана, исходя из параметров :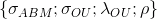


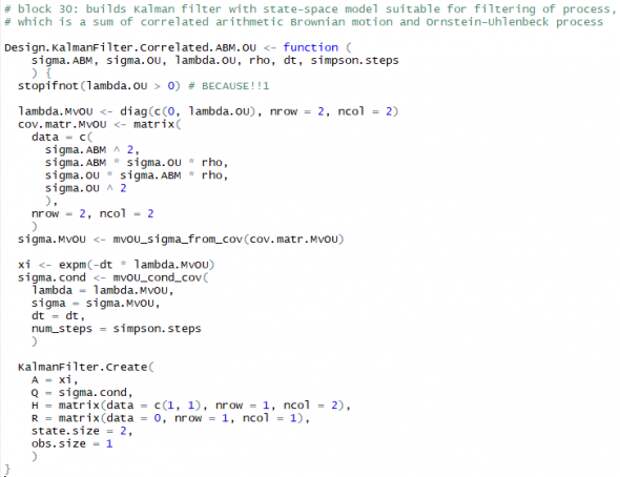
Как и в прошлый раз, сгенерируем синтетические данные и пройдёмся по ним фильтром Калмана:

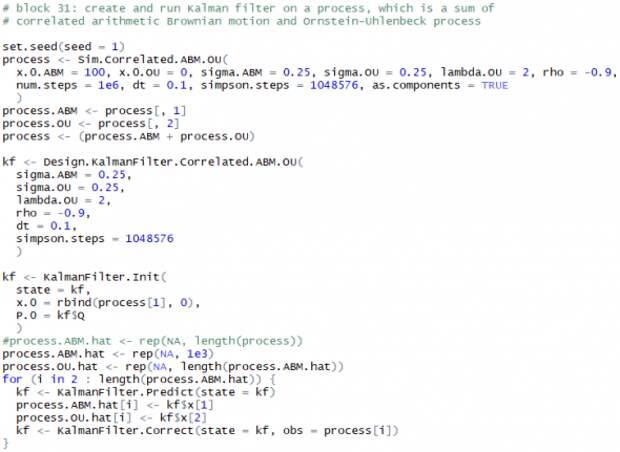
Ниже представлен график реализации процесса Correlated.ABM+OU (чёрный), оценки ABM компоненты фильтром Калмана (красный) и истинного значения ABM компоненты (зелёный). И опять на нём ничего не видно.


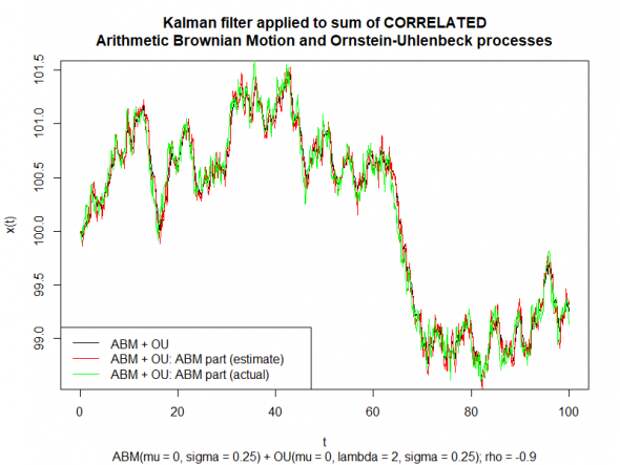
Ниже представлен график оценки OU компоненты фильтром Калмана (красный) и истинного значения OU компоненты (зелёный).


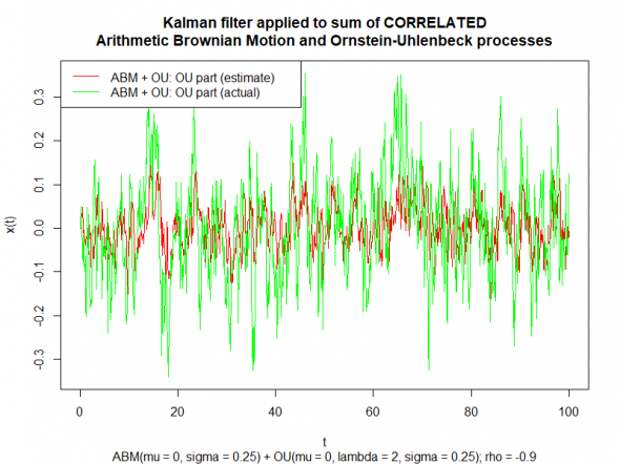
Построим scatter plot на основе данных с предыдущего графика:


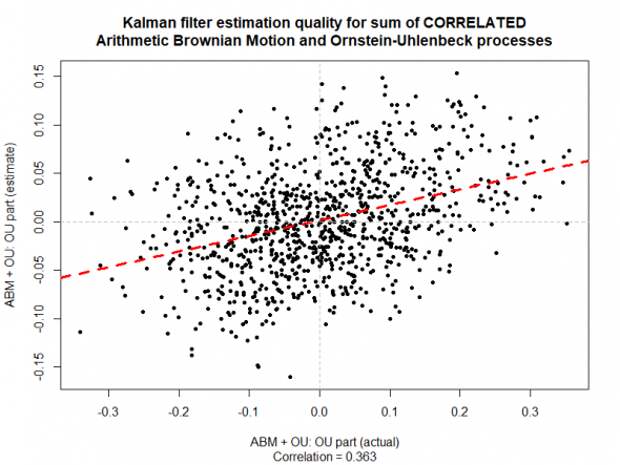
Заложенная в фильтр Калмана модель процесса вновь позволяет отделить средневозвратный процесс (OU) от арифметического Броуновского движения (ABM).

Что дальше

1. Попробовать применить метод разделения Independent.ABM+OU на компоненты к котировкам отдельных инструментов или линейных комбинаций (портфелей) инструментов;
2. Доделать механизм оценивания параметров для процесса Correlated.ABM+OU;
3. Посмотреть на модели с негауссовыми инновациями или модели с более сложной динамикой; использовать UKF/EKF/PF для оценивания компонент процесса;
4. Бросить всё и пойти пить пиво;
5. ???
6. Profit!

Приложения

Это раз
Это два