На прошлой неделе я опубликовал часть1 и часть2 статьи под общим названием с текущей. Обильная переписка в комментариях дала материал для настоящего эпилога. Публикую этот материал с дополнениями и исправлениями — убрав традиционный для СЛ срач))).
Один из «сильных» аргументов против игры с нулевой суммой со стороны немалого числа оппонентов является разомкнутость системы, позволяющей постоянно наращивать размер игрового фонда.
«Нулевая сумма» означает только то, что каким бы ни был фонд игры, он перераспределяется между игроками сильно неравномерно. За вычетом вновь поступающих в него денег (от новых участников, от роста денежной массы, от хеджеров, дивидендов и конечного потребителя) остальные деньги делятся таким образом, что суперприбыли равны суперубыткам.
Игра с ненулевой суммой, как следует из обеих частей статьи, отвечает за совсем незначительную часть доходов игроков, и сделать прогноз по приращению цены в любой момент времени, исходя только из этого представления, невозможно. Прогнозировать же возможно лишь при, как говорят математики, приближении (то есть, грубом допущении), что ничего, кроме игры с нулевой суммой, на бирже не происходит. Понимая, что такое допущение не соответствует полностью действительности, приходится допускать вероятностный характер ценовых приращений и заботиться об ограничении убытков в сделках и правилах управления капиталом.
Если совсем грубо попытаться передать идею игры с нулевой суммой, то получится как то так:
1. Возьмем график любого актива за какой-то промежуток времени
2. Измерим абсолютное приращение цены за этот период в пунктах
3. «Распрямим» траекторию этого же актива за этот же период
4. Измерим длину этой траектории в пунктах
5. Поделим дину распрямленной траектории на абсолютное приращение за период
Полученный коэффициент в первом приближении показывает во сколько раз идея игры с нулевой суммой лучше описывает рынок чем он описывается с т.
зр. игры с ненулевой суммой.Облигации — одна из лучших, если не самая лучшая, иллюстрация игры с нулевой суммой, потому что заранее известен ее финал — выкуп к погашению по номиналу.
Какая, казалось бы, вообще игра в облигациях?! МинФин размещает ОФЗ по номиналу и платит купон 7% через год, выкупая облигации по номиналу. Где тут, мать его, «НОЛЬ»?))) Сплошной плюс!
Приглядимся, однако, к графику цены ОФЗ. 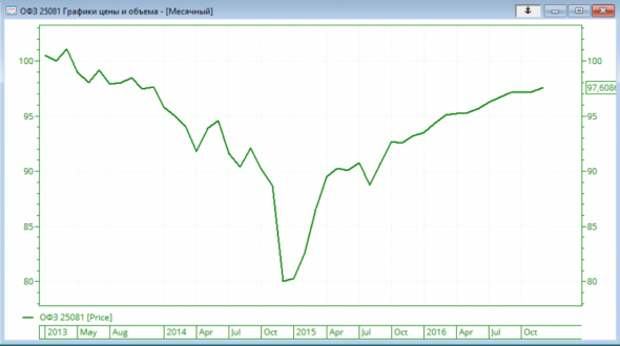
На данном графике видно, что абсолютное приращение с начала рассматриваемого периода до конца — примерно 3% (100 — 97), а длина траектории (даже без учета угла наклона и мелких колебаний) за тот же период — примерно 40 % (20 вниз и 20 наверх), итого идея с 0-й лучше идеи с не 0-й, грубо говоря, в 13 раз))).
Если конкретно: В самом большом наваре были покупатели по 80%, которые к погашению получат: номинал 100%, купон 7% и разницу в цене 20%.
В ненулевой игре максимальный доход — купон 7%. Откуда еще 20%? Ясно откуда — от продавцов по даунтренду, загнавших облигацию на 80%.
А чего это график такой неровный? Да потому что гоняют его спекулянты (и держатели тоже), в зависимости от слухов и фактов, касаемых:
а. надежности эмитента (РФ в нашем примере)
б. ключевой ставки ЦБ. Как только она снижается (или повышается вероятность снижения), то стоимость облигации растет, и тот, кто купил ее низко, имеет возможность продать ее высоко. И у того, кто купил ее с выгодой, есть контрагент, продавший ее с убытком.
при неизменных: номинале и величине купона.
Что важно для спекулянта?
Вспомним вместе принцип спекуляции: купить дешево-продать дорого/продать дорого-откупить дешево. А также вспомним определение игры — процесс с участием, минимум, двоих игроков, где действия первого зависят от действий второго, а действия второго — от действий первого.
«Купить дешево» предполагает, что после нашей покупки другие спекулянты тоже начнут покупать (причем, по цене предложения), и только тогда у нас появится возможность продать дороже. Те другие спекулянты, в свою очередь, тоже надеются, что после них продолжатся покупки.
Соответственно, нам нужна модель ценового движения, которая «предугадает» следующее приращение из какой-то области цены. А по сути — модель поведения игроков, ибо только они и являются источником ожидаемого приращения.
Возвращаемся к облигации.
Здесь мне придется вставить цитату из комментария ко второй части статьи:
Облигации 80% держателей не смотрят на изменчивость цены. им важен купон
Даже если бы это было правдой (а это неправда, потому что «держатели» очень ревностно относятся к изменчивости цен – если можно заработать 10%, зачем «настаивать» на 7%?), какое нам дело до тех, кто купил по номиналу, чтобы продать по номиналу с купоном? Эти держатели облигации вообще находятся вне игры (см. выше определение игры). Они не участвуют в формировании цены. Их может быть хоть 99,9%. Игра происходит между моментами размещения и погашения, и нас интересуют те оставшиеся ИГРОКИ – хоть 20% хоть 0,1% — которые участвуют в этой игре, формируя траекторию движения цены облигации, потому что заработать можно только на движении. Единственная возникающая в этом случае (малое количество спекулируемых облигаций) проблема — отсутствие ликвидности. И вот в этом самом процессе и происходит игра с нулевой суммой, в результате которой одни игроки заработают «лишних» 20%, а другие – их же проиграют.
И эта огромная разница – не только за счет убытков других спекулянтов этим же активом а, внимание!, за счет продажи низкодоходных облигаций «держателями» при появлении на рынке облигаций с более высоким доходом при росте ключевой ставки (это еще раз к вопросу про 80% держателей, «женившихся» на купоне)
Далее был комментарий про акции.
В акциях тоже самое. Ну не 80%, Ну пускай 60. Пускай 50/50. Значит нет игры с нулевой суммой в чистом виде.
Аналогичная ситуация с акциями. Мажоритарные акционеры могут держать у себя сколько угодно большой процент акций, но нас эти мажоритарии не волнуют. Нас интересуют акции во фрифлоте, которые торгуются каждый день. Будь это 30, 20 или 5% всех акций. В этом фрифлоте создаются и теряются состояния, не зависимо от того, что в систему (фонд игры) могут поступать деньги от новых игроков, дивидендов или QE. И в этом фрифлоте рисуется самая обычная спекулятивная траектория, смоделировать которую можно, лишь огрубив действительность до игры с нулевой суммой.