По мотивам… ну, вы сами поняли:)
Вместо пролога. Зачем нам волатильность? Зачем нам её приводить одну к другой и сравнивать? Её физический смысл — как далеко может убежать траектория случайного процесса. Надеюсь, на СЛ стало меньше людей, сомневающихся в том, что изменение цены и сама цена — процесс случайный?
Теперь цена. И в БШ и везде у нас для масштабирования волатильности используется квадратный корень.
А давайте посчитаем? Пойдем от обратного. Волатильности тут уже считали. И доказывали, что вся отлично выводится одно из другого путем взятия квадратного корня (хоть сперва на минутках посчитай минутную, хоть на дневках дневную). И это хорошо, посколько процесс один и хочется, чтобы волатильностей у него много не было — как ни считай. Правда нам уже и доказали, что не совсем это так и могут быть нюансы.
А мы давайте посчитаем вот что. Возьмем фРТС с 2005 года и будем его нарезать — сэмплировать на минутках. От часовых отрезков до нескольких дней. Каждый такой отрезок будем сдвигать вправо. И для каждого отрезка будем запоминать две величины: DP и DT. DP это насколько изменилась цена за данный отрезок, DT — сколько это заняло времени. Полный перебор сделать у меня, конечно, не получилось. Поэтому сэмплы я двигал по 20 минутных отсчетов и чем выше масштаб, тем меньше там получалось сэмплов. Итого:
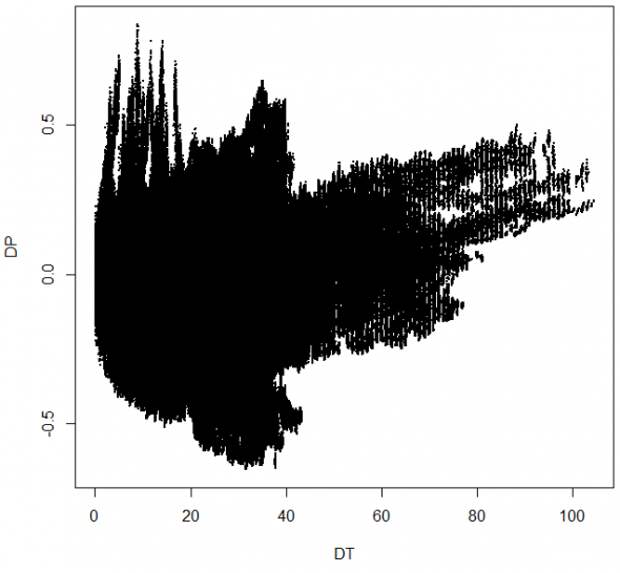
DT в днях. Сделаем абсциссу логарифмической:
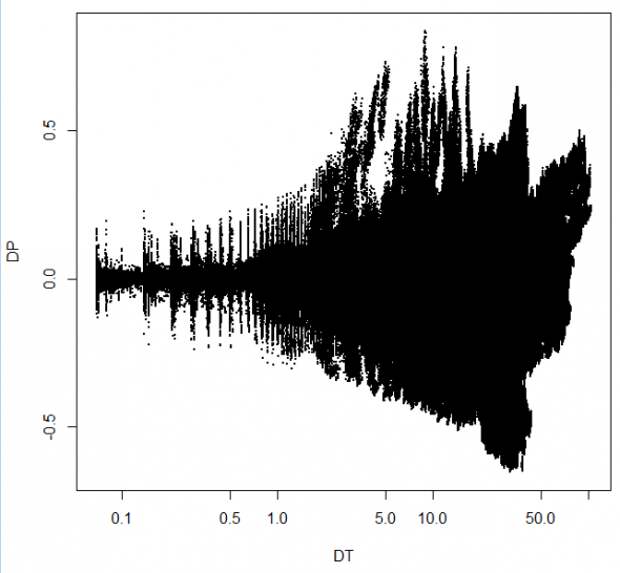
Ну вот мы и видим что-то такое нелинейное и вроде квадратичное. Оно и логично. Чем больше DT, тем больше будет DP, но вроде кажется, что как раз пропорционально квадратному корню. А давайте в малых окрестностях DT посчитаем сигмочки:
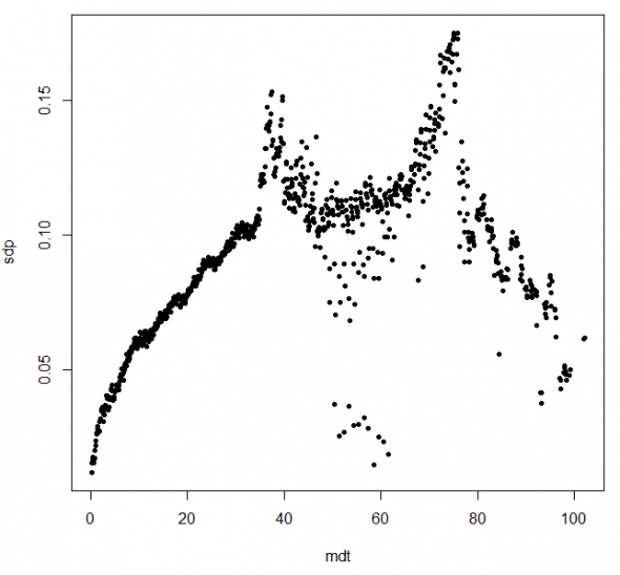
sdp это те самые волатильности, mdt это среднее значение DT для своей окрестности. После 30 дней совсем маленькие выборки, поэтому их отбросим и посчитаем желаемое:
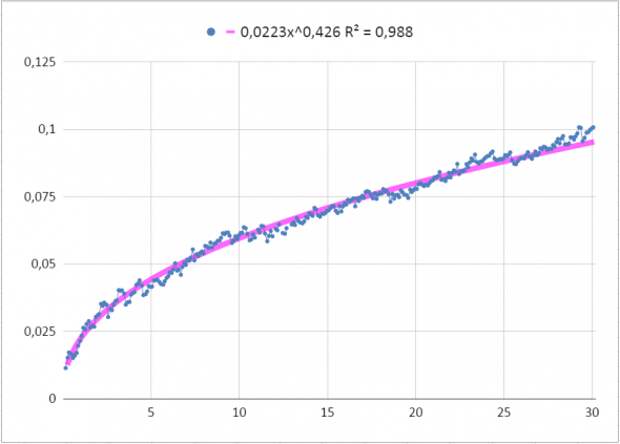
Лучшая аппроксимация из элементарных — степенная, но не квадратный корень…